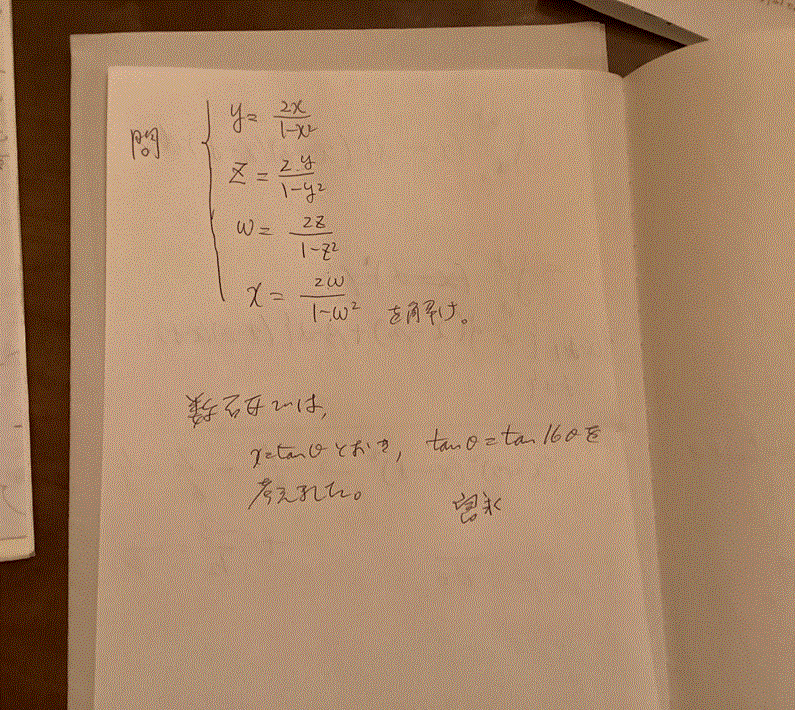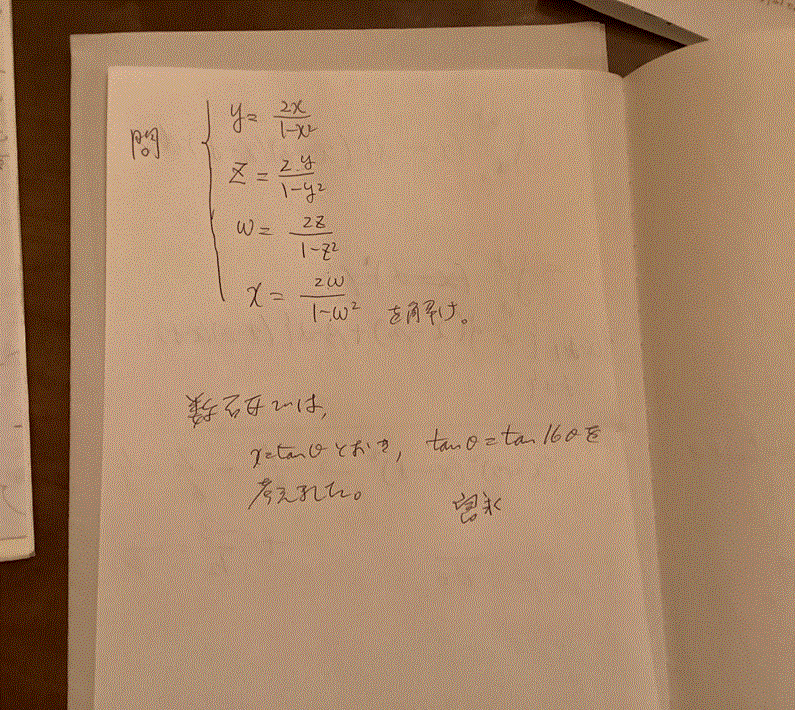正接の倍角公式は，

　　ｔａｎ２θ＝２ｔａｎθ／（１−ｔａｎ^2θ）

で与えられる．

　正接のｎ倍角公式は，パスカルの三角形を用いて，次のように書くことができる．

　　ｔａｎｎθ＝（nC1ｔａｎθ−nC3ｔａｎ^3θ＋nC5ｔａｎ^5θ−・・・）／（nC0−nC2ｔａｎ^2θ＋nC4ｔａｎ^4θ−・・・）

　分母・分子の係数は，２項係数の符号が対で交代するパスカルの正接三角形

　　　　　　　　　　　　１

　　　　　　　　　　１　　　１

　　　　　　　　１　　　２　　　−１

　　　　　　１　　　３　　　−３　　　−１

　　　　１　　　４　　　−６　　　−４　　　１

　　１　　　５　　−１０　　−１０　　　５　　　１

の形に並べることができる．ほとんどの教科書から消えてしまったが，美しい公式である．

　　ｔａｎ３θ＝（３ｔａｎθ−ｔａｎ^3θ）／（１−３ｔａｎ^2θ）

　　ｔａｎ４θ＝（４ｔａｎθ−４ｔａｎ^3θ）／（１−６ｔａｎ^2θ＋ｔａｎ^4θ）

　　ｔａｎ５θ＝（５ｔａｎθ−１０ｔａｎ^3θ＋ｔａｎ^5θ）／（１−１０ｔａｎ^2θ＋５ｔａｎ^4θ）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　ｔａｎnθ＝ｔａｎθを一般化してみたい。パスカルの正接三角形を使うと面倒になりそうなので、λ=exp(iθ)=cosθ+isinθとおく

λ+λ^-1=2cosθ、λ-λ^-1=2isinθ

λ^n+λ^-n=2cosnθ、λ^n-λ^-n=2isinnθ

tanθ=(λ-λ^-1)/i(λ+λ^-1)=(λ^2-1)/i(λ^2+1)

tannθ/2=2sinnθ/(2+2cosnθ)=(λ^n-λ^-n)/i(2+λ^n+λ^-n)=(λ^2n-1)/i(λ^n+1)^2=(λ^n-1)/i(λ^n+1)

tannθ=(λ^2n-1)/i(λ^2n+1)

tannθ=tanθ→(λ^2n-1)/(λ^2n+1)=(λ^2-1)/(λ^2+1)に帰着される。

μ=λ^2=exp(2iθ)とおくほうがよさそうである。

tannθ=tanθ→(μ^n-1)/(μ^n+1)=(μ-1)/(μ+1)に帰着される。

-(μ^n+1-1)-(μ^n-μ)=0

(μ-1){-2(μ^n-1+・・・μ^2+μ)}=0

(μ-1)=0または(μ^n-1+・・・μ^2+μ)=0

μ=0,(μ-1)=0または(μ^n-2+・・・μ^2+μ+1)=0→μ=cos(2π/(n-1))+isin(2π/(n-1))=cos(2θ)+isin(2θ）よりθが求まる

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

n=16の場合は正15角形の中心角を求める問題に帰着されるが、

これは正三角形と正五角形を重ねて作図した際の偏角の差として計算することができる。

cos(4π/5-2π/3)=cos4π/5cos3π/2+sin4π/5sin2π/3

したがって、θは正30角形の頂点の偏角となる。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

この問題の原文は

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
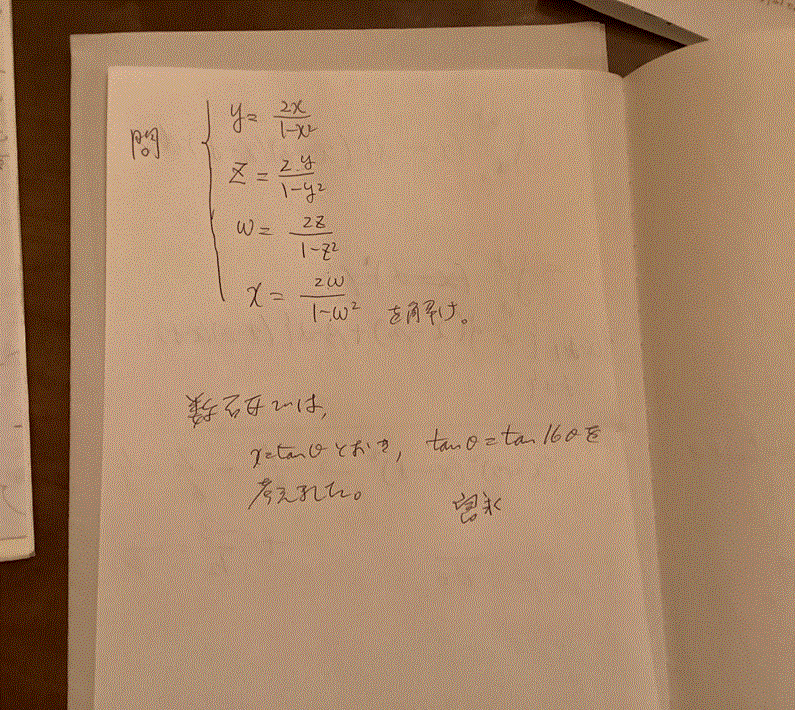